#26 - 02/2023

“τεχνητή νοημοσύνη”: μεγάλα γλωσσικά μοντέλα στην εποχή των «πνευματικών» περιφράξεων

Μπορούν [1Όλες οι εικόνες που συνοδεύουν το κείμενο, εκτός από τα διαγράμματα των νευρωνικών δικτύων, έχουν παραχθεί από μας με τη βοήθεια του DALL-E 2, ενός μοντέλου τεχνητής νοημοσύνης που παράγει εικόνες με βάση μια περιγραφή που δίνει ο χρήστης υπό τη μορφή κειμένου.] να γράφουν από μόνα τους ποιήματα και διηγήματα, μπορούν να συνομιλούν με έναν άνθρωπο με εντυπωσιακή φυσικότητα, έχουν ιδιαίτερη έφεση στο να γράφουν φοιτητικές εργασίες για λογαριασμό όσων φοιτητών προτιμούνε (μάλλον δικαίως) να ξοδεύουν αλλιώς τον χρόνο τους, έχουν ταλέντο στον προγραμματισμό και το αποδεικνύουν με το να γράφουν malware· εσχάτως έχουν υπάρξει σκέψεις να χρησιμοποιηθούν κατά τη διάρκεια μιας δίκης για να παρέχουν σε πραγματικό χρόνο νομικές συμβουλές. Όχι, δεν πρόκειται για τίποτα παιδιά – θαύματα που μεγάλωσαν και εκπαιδεύτηκαν σε μυστικά, υπόγεια εργαστήρια και τώρα βγήκαν στον κόσμο. Όλα αυτά είναι μερικά από τα κατορθώματα του ChatGPT, του GPT-3 και του LaMDA, μερικών εκ των πιο γνωστών συστημάτων τεχνητής νοημοσύνης για επεξεργασία (και παραγωγή) φυσικής γλώσσας που πρόσφατα έγιναν δημόσια διαθέσιμα (τουλάχιστον τα δύο πρώτα, αν και απαιτείται εγγραφή), δίνοντας έτσι αφορμή για να ξεκινήσει άλλος ένας κύκλος συζητήσεων περί του αν είμαστε κοντά στη δημιουργία «σκεπτόμενων μηχανών».

Είναι σχεδόν βέβαιο ότι τα συγκεκριμένα συστήματα, που ανήκουν στην κατηγορία των λεγόμενων μεγάλων γλωσσικών μοντέλων (large language models), θα μπορούσαν να περάσουν με επιτυχία το περιβόητο τέστ του Turing, τουλάχιστον υπό την προϋπόθεση ότι ο διάλογος θα ήταν σχετικά σύντομος. Το ένα ζήτημα που προκύπτει εδώ αφορά στο κατά πόσον το τεστ του Turing είναι όντως κατάλληλο για να κρίνεται η όποια «νοημοσύνη» ενός συστήματος. Αυτή είναι η πιο «συμπεριφορική» πλευρά του θέματος· ασχολούμαστε με το πώς συμπεριφέρεται κάτι, ασχέτως του πώς φτάνει σε αυτήν τη συμπεριφορά. Ένα άλλο ζήτημα, ωστόσο, αφορά ακριβώς σε αυτό το «πώς», στην εσωτερική λειτουργία αυτών των γλωσσικών μοντέλων που τους επιτρέπει να διεξάγουν τόσο αληθοφανείς διαλόγους. Πέρα από την όποια αυταξία μπορεί να έχει μια τέτοια γνώση του «εσωτερικού κόσμου» αυτών των μοντέλων, σίγουρα βοηθάει και στην απομυθοποίησή τους. Το να προσφέρει κανείς ως εξήγηση φράσεις σαν «πρόκειται για μοντέλα που βασίζονται σε βαθιά νευρωνικά δίκτυα που χρησιμοποιούν μετασχηματιστές» μάλλον δεν χρησιμεύει ιδιαίτερα· αντιθέτως ίσως να εντείνει το αίσθημα το μυστηρίου. Για να γίνει καλύτερα κατανοητή η εσωτερική δομή τους, χρειάζεται να κάνει κανείς πρώτα λίγα βήματα πιο πίσω.

Έστω, λοιπόν, ότι καλούμαστε να λύσουμε το ακόλουθο μαθηματικό πρόβλημα (μην τρομάζετε όσοι δεν είστε ιδιαίτερα εξοικειωμένοι με τα μαθηματικά· μόνο προσθέσεις και πολλαπλασιασμοί απαιτούνται για την κατανόηση όσων ακολουθούν). Μας δίνεται η εξίσωση w1 χ a1 + w2 χ a2 = b, όπου a1, a2 και b είναι μεταβλητές, με τις a1 και a2 να παίρνουν μόνο δύο τιμές: είτε 0 είτε 1. Ο σκοπός είναι να βρούμε κατάλληλες τιμές για τις παραμέτρους w1 και w2 ώστε, όποτε όταν οι a1 και a2 παίρνουν και οι δύο την τιμή 1, η τιμή της b να υπερβαίνει κάποιο δεδομένο όριο, έστω το 10. Σε διαφορετική περίπτωση, αν κάποια από τις a1 ή a2 (ή και οι δύο) έχουν την τιμή 0, τότε θα πρέπει η τιμή της b να είναι κάτω από το 10. Για καλύτερη και εποπτικότερη κατανόηση, το πρόβλημα μπορεί να αποτυπωθεί υπό τη μορφή πίνακα ως εξής:

a1	a2	b
1	1	>10
1	0	<10
0	1	<10
0	0	<10

Με μερικές δοκιμές είναι εύκολο να βρεθεί μια λύση σε αυτό το πρόβλημα. Για παράδειγμα, θα μπορούσαμε να επιλέξουμε ως λύση την εξής: w1 = 5 και w2 = 6. Επομένως, η αρχική μας εξίσωση γίνεται 5 x a1 + 6 x a2 = b. Δοκιμάζοντας όλους τους συνδυασμούς για τις a1 και a2, είναι δυνατό να επιβεβαιώσουμε ότι αυτή είναι πράγματι μια λύση του προβλήματός μας. Αν, π.χ., θέσουμε a1 = 1 και a2 = 1, τότε λαμβάνουμε το αποτέλεσμα 5 x 1 + 6 x 1 = 5+6 = 11, όπως και θα έπρεπε. Αντιστοίχως, αν a1 = 1 και a2 = 0, τότε προκύπτει ότι b = 5 x 1 + 6 x 0 = 5. Για a1 = 0 και a2 = 1, προκύπτει ότι b = 6. Τέλος, για a1 = 0, a2 = 0, προκύπτει b = 0. Υπάρχουν φυσικά και άλλες λύσεις στο πρόβλημα (π.χ., w1=8 και w2=7), ωστόσο το σημαντικό είναι ότι καταφέραμε να βρούμε έστω μία.

Αν μπορέσατε να ακολουθήσετε την παραπάνω συλλογιστική και λύσατε το αρχικό πρόβλημα, τότε συγχαρητήρια! Μόλις χρησιμοποιήσατε ένα νευρωνικό δίκτυο για να προσομοιώσετε τον τελεστή ΚΑΙ (AND) της άλγεβρας Boole και μπορείτε να ισχυρίζεστε ότι φτιάξατε έναν μικρό εγκέφαλο με την ικανότητα λογικών συλλογισμών. Αν βέβαια επιχειρούσε κανείς να θέσει το πρόβλημα χρησιμοποιώντας τέτοιους βαρύγδουπους όρους, είναι λογικό ότι κανένας «αγεωμέτρητος» δεν θα ήταν σε θέση όχι μόνο να το επιλύσει αλλά και να καταλάβει περί τίνος πρόκειται. Ένα συνηθισμένο τέχνασμα εξάλλου της σχετικής φιλολογίας γύρω από την τεχνητή νοημοσύνη που παράγεται με πληθωριστικούς ρυθμούς πλέον είναι ακριβώς η επιστράτευση μιας ακατανόητης γλώσσας, απρόσιτης στους αμύητους, η οποία συχνά προσάγεται σχεδόν ως τεκμήριο που αποδεικνύει τόσο τη σπουδαιότητα του προβλήματος («να φτιάξουμε ευφυείς μηχανές») όσο και των προτεινόμενων λύσεων («να τις κάνουμε να μοιάζουν με τον εγκέφαλο»). Στην πραγματικότητα βέβαια, αν και οι τεχνικές και μαθηματικές λεπτομέρειες ενδέχεται όντως να είναι εξαιρετικά πολύπλοκες, οι βασικές ιδέες δεν χρειάζεται σε καμμία περίπτωση να περιβάλλονται με την ερεβώδη αχλή του μυστηριώδους (σε αντίθεση, π.χ., με την κβαντομηχανική και τη σχετικότητα οι οποίες είναι πράγματι δύσκολο να συλληφθούν όχι μόνο μαθηματικά αλλά ακόμα και εννοιολογικά).

Πώς ακριβώς λοιπόν μια εξίσωση του τύπου w1 x a1 + w2 x a2 = b μπορεί να αντιστοιχεί σε ένα νευρωνικό δίκτυο που μάλιστα μπορεί να εκτελεί πράξεις λογικού συμπερασμού; Πρώτον, πρέπει να γίνει κατανοητό τι ακριβώς είναι η άλγεβρα Boole. Παρότι όχι τόσο γνωστός στο ευρύτερο κοινό όσο άλλοι σπουδαίοι μαθηματικοί, ο Boole (1815 - 1864) δικαιωματικά κατέχει μεταξύ των ειδικών μια ιδιαίτερη θέση μέσα στην ιστορία των μαθηματικών. Η θεωρία του δεν διακρίνεται ούτε για τη στρυφνότητά της ούτε για τη χρήση περίπλοκων και τρομακτικών μαθηματικών εργαλείων. Το επίτευγμά του κρίνεται σημαντικό κυρίως σε ένα εννοιολογικό επίπεδο. Αυτό που κατάφερε, λοιπόν, ο Boole ήταν να συλλάβει την ιδέα ότι η κλασσική, προτασιακή λογική (αυτή που ήταν γνωστή ήδη από τον Αριστοτέλη) μπορεί να λάβει μια αλγεβρική μορφή. Με άλλα λόγια, να διατυπωθεί υπό τη μορφή εξισώσεων οι οποίες επιδέχονται επίλυση με βάση κάποιους βασικούς κανόνες, σε μεγάλο βαθμό όπως και οι τυπικές εξισώσεις της κλασσικής άλγεβρας οι οποίες χειρίζονται πραγματικούς αριθμούς.

Η βασική διαφορά σε σχέση με την άλγεβρα Boole είναι ότι σε αυτήν την τελευταία οι μεταβλητές (a, b, κ.ο.κ.) παίρνουν μόνο δύο τιμές, είτε 1 είτε 0. Κατά κανόνα, το 1 αντιστοιχεί σε αυτό που στη λογική είναι η αληθοτιμή ΑΛΗΘΕΣ (TRUE), ενώ το 0 στο ΨΕΥΔΕΣ (FALSE). Έχοντας ως βάση αυτή τη σύμβαση, μπορούμε να χρησιμοποιήσουμε τα σύμβολα των πράξεων (π.χ., της πρόσθεσης και του πολλαπλασιασμού) για να διατυπώσουμε λογικές προτάσεις υπό τη μορφή εξισώσεων.

Για παράδειγμα, έστω ότι έχουμε τις προτάσεις p, q και r (όπου το p σημασιολογικά μπορεί να σημαίνει ότι «ο Σωκράτης είναι άνθρωπος» και κάτι παρόμοιο για τα q και r) και θέλουμε να πούμε ότι το r ισχύει (δηλαδή είναι αληθές) μόνο αν ισχύουν ταυτόχρονα και το p και το q. Μια τέτοια πρόταση μπορεί να γραφτεί στην άλγεβρα Boole ως p x q = r, όπου εδώ το σύμβολο του πολλαπλασιασμού χρησιμοποιείται για να υποδηλώσει τη λογική σύζευξη (ΚΑΙ, AND). Η λογική διάζευξη (το r ισχύει μόνο αν τουλάχιστον ένα από τα p και q ισχύει), από την άλλη, μπορεί να γραφτεί ως p + q = r, όπου εδώ δίνεται ένα νέο νόημα στο σύμβολο της πρόσθεσης. Αν επομένως, στην πρόταση p x q = r θέσουμε ως p = 1 και q = 1, τότε προκύπτει ότι r = 1. Σε κάθε άλλη περίπτωση, θα ισχύει ότι r = 0. Ξεκινώντας από τέτοιους βασικούς κανόνες, είναι δυνατό να κατασκευαστούν λογικές προτάσεις μεγάλης πολυπλοκότητας, με πολλαπλούς συνδυασμούς των διαφόρων τελεστών. Επειδή ακριβώς πέτυχε να τυποποιήσει τη λογική, η άλγεβρα Boole αποτέλεσε και το πρώτο μεγάλο βήμα προς τη μηχανοποίησή της· σήμερα όλα τα ψηφιακά κυκλώματα βασίζονται σε αυτήν.

Από τα παραπάνω, είναι μάλλον προφανές γιατί η εξίσωση w1 x a1 + w2 x a2 = b, με τα κατάλληλα βάρη w1 και w2, αντιστοιχεί σε μια εξίσωση Boole. Για την ακρίβεια, αντιστοιχεί στην πράξη της λογικής σύζευξης. Οποτεδήποτε οι μεταβλητές a1 και a2 παίρνουν και οι δύο την τιμή 1, η έξοδος (δηλαδή η μεταβλητή b) παίρνει μια τιμή μεγαλύτερη από ένα κατώφλι. Σε κάθε άλλη περίπτωση, η τιμή της είναι κάτω από αυτό το κατώφλι. Το 10 στην προκειμένη περίπτωση είναι εντελώς αυθαίρετο και θα μπορούσε να είχε αντικατασταθεί με οποιονδήποτε άλλο αριθμό. Το βασικό είναι η γενική συμπεριφορά της εξίσωσης: η υπέρβαση του κατωφλίου ερμηνεύεται ως 1 και κάθε άλλη έξοδος ως 0.

Το δεύτερο ζήτημα που χρειάζεται διευκρίνιση είναι το πώς η εξίσωση w1 x a1 + w2 x a2 = b μπορεί να αντιστοιχεί σε ένα νευρωνικό δίκτυο. Το πιο βασικό και απλό νευρωνικό δίκτυο είναι το λεγόμενο perceptron και αποτελείται από έναν μοναδικό κόμβο – νευρώνα. Αυτός δέχεται μια σειρά από εισόδους (a1, a2, κ.ο.κ) και καθεμία από αυτές τις εισόδους συνοδεύεται και από ένα βάρος (w1, w2, κ.ο.κ. αντίστοιχα). Αυτό που κάνει ο κόμβος είναι να πολλαπλασιάζει κάθε είσοδο με το αντίστοιχο βάρος της (w1 x a1, w2 x a2, κ.ο.κ.), μετά να προσθέτει όλα τα επιμέρους αποτελέσματα των πολλαπλασιασμών (w1 x a1 + w2 x a2 + …) για να παραγάγει μια πρώτη έξοδο b και στο τέλος να περνάει αυτήν την έξοδο από ένα κατώφλι, όπως έχουμε ήδη περιγράψει. Πειράζοντας τώρα τα διάφορα βάρη, μπορούμε να «σπρώξουμε» το perceptron προς μια επιθυμητή συμπεριφορά, π.χ., να προσομοιώνει τη λογική σύζευξη, τη λογική διάζευξη ή άλλες πράξεις λογικού (και μη) τύπου. Το πείραγμα των βαρών αυτών προς συγκεκριμένη κατεύθυνση είναι αυτό που στη σχετική φιλολογία αποκαλείται «εκπαίδευση» του δικτύου και φυσικά δεν εκτελείται χειροκίνητα (όπως απλουστευτικά παρουσιάσαμε παραπάνω), αλλά με κατάλληλους αλγορίθμους.

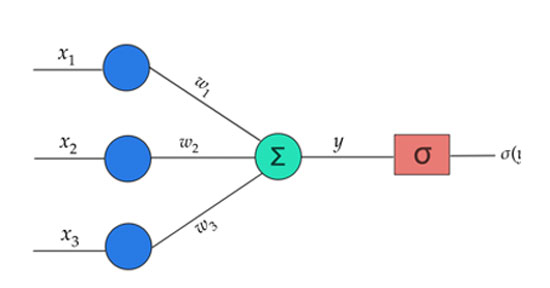
Ένα βασικό ερώτημα που ανακύπτει σε αυτό το σημείο έχει να κάνει με το γιατί μια τέτοια σειρά μαθηματικών πράξεων (πολλαπλασιασμοί, πρόσθεση, κατώφλι) να αποκαλείται «νευρώνας». Τι σχέση μπορεί να έχει με τους πραγματικούς νευρώνες του εγκεφάλου;
Ένα διαφορετικό όνομα για το perceptron είναι και νευρώνας τύπου McCulloch – Pitts από τους δύο επιστήμονες που τον πρότειναν ως ιδέα το 1943. Ο λόγος για τον οποίο η συγκεκριμένη μαθηματική δομή χαρακτηρίστηκε ως «νευρώνας» αφορά στην ομοιότητα που υποτίθεται ότι παρουσιάζει προς τους πραγματικούς, βιολογικούς νευρώνες. Οι πρώτες πειραματικές παρατηρήσεις για τη λειτουργική συμπεριφορά των βιολογικών νευρώνων είχαν δείξει ότι οι συνάψεις που επικολλώνται πάνω σε έναν νευρώνα μεταφέρουν ηλεκτρικούς παλμούς προς αυτόν από τους προηγούμενούς του. Ο νευρώνας που δέχεται αυτούς τους παλμούς φαίνεται σαν να αθροίζει τα εισερχόμενα σήματα και αν η συνολική τους ισχύ (η οποία εξαρτάται και από το πόσο ισχυρές είναι οι συνάψεις) ξεπεράσει ένα κατώφλι, τότε εκπυρσοκροτεί και αυτός με τη σειρά του. Με αυτόν τον τρόπο μεταφέρει κατά μήκος του νευράξονά του έναν νέο ηλεκτρικό παλμό προς τους επόμενους νευρώνες, η ισχύς του οποίου όμως παραμένει πάντα σταθερή (κάποια δεκάδες mV), ανεξαρτήτως του πόσα και πόσο ισχυρά σήματα δέχτηκε ως ερεθίσματα. Συγκρίνοντας επομένως έναν βιολογικό νευρώνα με το perceptron, κάποιες ομοιότητες είναι προφανείς. Οι μεταβλητές a αντιστοιχούν στα ερεθίσματα – παλμούς που δέχεται ένας βιολογικός νευρώνας, τα βάρη w αντιστοιχούν στις συνάψεις και η τελική πράξη του κατωφλίου αντιστοιχεί στον «κόφτη» που επιβάλλει ένας νευρώνας στο ύψος του παλμού που παράγει αν τελικά εκπυρσοκροτήσει.Το perceptron ήταν μια πρώτη, πρωτόλεια απόπειρα να μοντελοποιηθούν οι πραγματικοί νευρώνες.

Εννοείται βέβαια πως από το 1943 και μετά έχει κυλήσει πολύ νερό στο αυλάκι της επιστημονικής έρευνας πάνω στα «μυστικά του εγκεφάλου». Σπανίως πλέον χρησιμοποιούνται τα perceptron ως ρεαλιστικοί προσομοιωτές των βιολογικών νευρώνων. Τα πιο σύγχρονα νευρωνικά μοντέλα επιστρατεύουν ένα πλήθος διαφορικών εξισώσεων που είναι αρκετά πιο απαιτητικές για την επίλυσή τους από μερικούς πολλαπλασιασμούς και μια πρόσθεση. Οι νευρώνες τύπου perceptron, σε διάφορες παραλλαγές, εξακολουθούν να χρησιμοποιούνται, αλλά όχι για την μοντελοποίηση βιολογικών λειτουργιών του εγκεφάλου. Αυστηρά μιλώντας, δεν πρόκειται καν για δίκτυα, εφόσον αποτελούνται από έναν και μόνο κόμβο. Ωστόσο, η χρησιμότητά τους έγκειται κατά κύριο λόγο στο ότι αποτελούν τις βασικές δομικές μονάδες για την κατασκευή τεχνητών νευρωνικών δικτύων τα οποία εκπαιδεύονται για να επιλύσουν προβλήματα μηχανικής μάθησης (π.χ., η αναγνώριση οδικών σημάτων στους δρόμους) χωρίς κάποια ιδιαίτερη δέσμευση όσον αφορά στην απομίμηση του τρόπου που ο ανθρώπινος εγκέφαλος λειτουργεί πάνω στα ίδια προβλήματα. Για τα ίδια τα perceptron, στη μορφή που έχουν ως μεμονωμένοι κόμβοι, έγινε σχετικά γρήγορα αντιληπτό ότι έχουν σοβαρούς περιορισμούς (π.χ., αποδείχτηκε μαθηματικά ότι τους είναι αδύνατο να επιλύσουν την λογική πράξη του XOR, δηλαδή της αποκλειστικής διάζευξης κατά την οποία η έξοδος πρέπει να είναι 1 αν μόνο μία και ακριβώς μία από τις εισόδους είναι 1 και η άλλη 0). Τέτοιου είδους προβλήματα αντιμετωπίστηκαν με την εισαγωγή των καθαυτό νευρωνικών δικτύων, όπως τα multi-layer perceptron, τα οποία αποτελούνται από πολλαπλούς κόμβους, διατεταγμένους σε αλλεπάλληλα επίπεδα με τις εξόδους του κάθε επιπέδου να τροφοδοτούν τις εισόδους του επομένου. Κομβικής σημασίας υπήρξε επίσης το γεγονός ότι τη δεκαετία του 1980 ανακαλύφθηκε επιτέλους κι ένας «ορθός» και αποδοτικός τρόπος ώστε να εκπαιδεύονται τα συγκεκριμένα δίκτυα (δηλαδή να ορίζονται οι τιμές των βαρών που έχουν οι συνδέσεις μεταξύ των κόμβων). Όπως είναι ευνόητο, οι παραλλαγές εδώ είναι απειράριθμες. Το πόσα επίπεδα θα έχει ένα δίκτυο, πόσους νευρώνες θα έχει κάθε επίπεδο, αν ένας νευρώνας θα τροφοδοτεί όλους του επόμενου επιπέδου ή μόνο μερικούς από αυτούς, αν κάποιοι νευρώνες θα έχουν τη δυνατότητα να προσπερνάνε το αμέσως επόμενο επίπεδο και να συνδέονται με κάποιο άλλο σε μεγαλύτερο βάθος ή ακόμα και αν θα έχουν ανάστροφη φορά ώστε αγκιστρώνονται σε προηγούμενα ή και στο ίδιο επίπεδο· όλα αυτά αποτελούν μόνο μερικές από τις σχεδιαστικές επιλογές που καλείται να κάνει ένας σύγχρονος μηχανικός, αναλόγως του προβλήματος που έχει να λύσει.

Στον βαθμό που τα νευρωνικά δίκτυα συνιστούν στατιστικά μοντέλα (όσο πιο συχνά εμφανίζονται συγκεκριμένα πρότυπα που πρέπει να μάθουν τόσο περισσότερο ενισχύονται ή καταστέλλονται τα κατάλληλα βάρη), η είσοδός τους οφείλει να είναι μια σειρά από αριθμούς. Παρ’ όλα αυτά, δεν δουλεύουν μόνο με αριθμητικά δεδομένα. Για παράδειγμα, χρησιμοποιούνται κατά κόρον για να «διαβάζουν» (ή ακόμα και να παράγουν) εικόνες ή ηχητικά σήματα. Αυτό είναι εφικτό εφόσον πρώτα το αρχικό σήμα (εικόνα ή ήχος) μετατραπεί σε μια σειρά από αριθμούς· οι εικόνες μετατρέπονται σε αριθμούς που καθένας τους αναπαριστά ένα πίξελ και την έντασή του και οι ήχοι αναλόγως σε αριθμούς που αναπαριστούν την ένταση του ηχητικού σήματος. Εκτός από εικόνες και ήχους όμως, μπορούν να χειρίζονται και κειμενικά (μη ηχητικά) δεδομένα. Το πώς ακριβώς μετατρέπεται μια σειρά από γράμματα σε αριθμούς δεν είναι τόσο προφανές όσο στην περίπτωση οπτικοακουστικών δεδομένων, χωρίς πάντως αυτό να αποτελεί κάποιο ανυπέρβλητο εμπόδιο. Μια απλή μέθοδος μετατροπής είναι να αντιστοιχεί κάθε γράμμα ενός αλφαβήτου σε ένα «διάνυσμα» δυαδικών τιμών, δηλαδή σε μια σειρά από 0 και 1. Το a, π.χ., αντιστοιχεί στη σειρά [1 0 0 …] που έχει ένα 1 στην πρώτη θέση και 0 στις υπόλοιπες 25, το b στο [0 1 0 …] κ.ο.κ. Στην πράξη χρησιμοποιούνται λίγο πιο περίπλοκες τεχνικές αντιστοίχησης μεταξύ γραμμάτων και αριθμών (όπως τα λεγόμενα embedding). Σε κάθε περίπτωση πάντως, σημασία εδώ έχει ότι είναι όντως δυνατή αυτή η αντιστοίχηση, κάτι που με τη σειρά του σημαίνει ότι τα νευρωνικά δίκτυα μπορούν να εκπαιδευτούν πάνω και σε γλωσσικά δεδομένα.

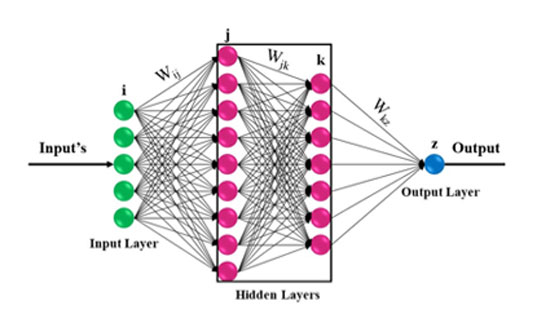
Για ποιους σκοπούς; Η πιο απλή περίπτωση είναι η χρήση τέτοιων μοντέλων για την αυτόματη διόρθωση κειμένων. Μια πιο απαιτητική εφαρμογή είναι η αυτόματη μετάφραση μεταξύ γλωσσών. Οι τιμές για το πιο εντυπωσιακό μέχρι στιγμής παράδειγμα χρήσης ωστόσο μάλλον θα έπρεπε να αποδοθούν στα λεγόμενα «μεγάλα γλωσσικά μοντέλα» (large language models), όπως το ChatGPT και το GPT-3 του OpenAI. Τα συγκεκριμένα μοντέλα έχουν την ικανότητα να παράγουν αυτόματα κείμενο είτε επεκτείνοντας ένα αρχικό κείμενο που δίνει ο χρήστης είτε ακόμα και απαντώντας σε ερωτήσεις ή εν γένει προτάσεις του χρήστη. Ο λόγος για τον οποίο έχουν κάνει μεγάλη αίσθηση είναι γιατί τα κείμενα που παράγουν διακρίνονται σχεδόν πάντα για την απόλυτη συντακτική ορθότητά τους (όσοι είχατε ασχοληθεί με τα πρώτα μεταφραστικά εργαλεία του είδους ίσως θυμάστε ότι το μεταφρασμένο κείμενο είχε συχνά συντακτικές αρρυθμίες) όπως επίσης και επειδή διαθέτουν μια (τουλάχιστον σε πρώτη ανάγνωση) νοηματική συνοχή, δίνοντας έτσι την εντύπωση ότι άνετα θα μπορούσαν να επιτύχουν στο τεστ του Turing με την φυσικότητα και την «ευφράδειά» τους [2Βλ. σχετικά και το άρθρο «Σκάνδαλο LaMDA (βλέπουν εφιάλτες τα νευρωνικά τεχνοδίκτυα;)», cyborg 25.].

Από καθαρά τεχνική άποψη, το επίσης εντυπωσιακό με τα μεγάλα γλωσσικά μοντέλα είναι ότι τα κατορθώματά τους δεν οφείλονται στη χρήση λεξικών ή γλωσσικών (συντακτικών, γραμματικών, σημασιολογικών) κανόνων. Κανένας δεν τα έχει προγραμματίσει με κανόνες του τύπου «μετά το υποκείμενο ακολουθεί το ρήμα και τέλος το αντικείμενο». Ό,τι κανόνες χρησιμοποιούν, τους μαθαίνουν έμμεσα, μέσα από τα κείμενα στα οποία έχουν εκπαιδευτεί. Μετά την εκπαίδευσή τους, αυτοί οι κανόνες έχουν «κωδικοποιηθεί» στα βάρη τους, αν και στην πραγματικότητα παραμένει εξαιρετικά δύσκολο να εντοπίσει κανείς τα βάρη που αντιστοιχούν στον τάδε ή στον δείνα κανόνα. Η συγκεκριμένη ασάφεια καθιστά αυτά τα μοντέλα κάπως «αδιαφανή», από την άποψη ότι δεν υπάρχει δυνατότητα να επεξηγηθεί η συμπεριφορά τους με έναν ανθρωπίνως κατανοητό τρόπο. Ανεξαρτήτως τέτοιων ερμηνευτικών ζητημάτων πάντως, το σημαντικό είναι ότι τα επιτεύγματά τους βασίζονται καθαρά στην ανακάλυψη στατιστικών κανονικοτήτων μέσα στα κείμενα που έχουν ήδη δει. Όταν ένας χρήστης ζητάει από το ChatGPT «να γράψει μια ιστορία σε τρεις παραγράφους με μάγους, νάνους, ξωτικά και ιππότες», αυτό ανταποκρίνεται πρόθυμα (ίσως δίνοντας και πρωτότυπα ονόματα στους ήρωες) επειδή ήδη έχει καταναλώσει αντίστοιχα κείμενα, έχει φτιάξει ένα απόθεμα από κατάλληλες φράσεις (μαζί με το τι συνήθως προηγείται και ακολουθεί κάθε φράσης) και μπορεί να τις ανακαλέσει, να τις συγκολλήσει και να τις ανασυνδυάσει με ποικίλους τρόπους. Για να είναι επιτυχής (δηλαδή αληθοφανής) αυτή η διαδικασία, προφανώς απαιτείται ένας τεράστιος όγκος κειμενικών δεδομένων για την εκπαίδευση των μοντέλων και τη δημιουργία ενός επαρκούς αποθεματικού τυποποιημένων φράσεων. Κάτι που με τη σειρά του συνεπάγεται ότι απαιτούνται και ογκώδη (από την άποψη του αριθμού νευρώνων) γλωσσικά μοντέλα, τέτοια που να διαθέτουν την κατάλληλη «χωρητικότητα» ώστε να αποθηκεύουν πολλαπλούς συνδυασμούς από ακολουθίες λέξεων για να τις συνδυάζουν και να παράγουν την αίσθηση του πρωτοτύπου. Τα σημερινά μοντέλα έχουν φτάσει στο σημείο να στοιβάζουν εκατοντάδες επίπεδα νευρώνων το ένα μετά το άλλο (εξ αυτού του λόγου καλούνται «βαθιά» δίκτυα), με τον συνολικό αριθμό των παραμέτρων – βαρών να ανέρχεται σε μερικά δισεκατομμύρια.

Όπως το έχει διατυπώσει ο Gary Marcus, ένας από τους πρωτοπόρους στον τομέα της τεχνητής νοημοσύνης (και ελαφρώς επικριτικός απέναντι στην τάση των τελευταίων χρόνων να χρησιμοποιούνται αποκλειστικά νευρωνικά δίκτυα εις βάρος άλλων μεθόδων), τα νευρωνικά δίκτυα που βρίσκονται πίσω από τα γλωσσικά μοντέλα είναι οι «άρχοντες του παστίς». Αυτό που παράγουν είναι μεν ένα στατιστικό προϊόν, αλλά όχι ακριβώς τυχαίο, αν με την έννοια αυτή εννοεί κανείς ότι ακόμα κι ένας πίθηκος μπροστά σε μια γραφομηχανή ίσως τελικά μπορεί κάποια στιγμή να «γράψει» ένα ποίημα του Μπόρχες. Ένα τέτοιο μοντέλο, σε αντίθεση με έναν πίθηκο που πατάει τυχαία πλήκτρα, δεν θα γράψει ποτέ μια τελείως ασυνάρτητη σειρά γραμμάτων (κάτι σαν «ψλομφ, γγφκπ οειφμψα»), χωρίς όμως αυτό να σημαίνει ότι παράγει κείμενο κατόπιν «σκέψης». Η έξοδός τους παράγεται καθαρά στατιστικά, μέσω κειμενικής κοπτοραπτικής. Η μεγάλη αληθοφάνεια των κειμένων τους οφείλεται ακριβώς στην υψηλή συνδυαστική ικανότητά τους.

Από την άλλη, αυτό είναι και ένα από τα αδύναμα σημεία τους. Εφόσον δεν διαθέτουν κάποια ικανότητα εκτέλεσης συλλογισμών, όταν διαπράττουν σφάλματα, αυτά συχνά είναι τερατώδη και παιδιάστικα· ο χρήστης ρωτάει «τι είναι βαρύτερο, ένα κιλό ατσάλι ή ένα κιλό βαμβάκι;» και το μοντέλο απαντάει με αυτοπεποίθηση και «επιχειρήματα» ότι φυσικά το ένα κιλό ατσάλι είναι βαρύτερο επειδή κάπου μέσα στα κείμενα που έχει καταναλώσει το ατσάλι πάντα θεωρείται βαρύτερο από το βαμβάκι.
Την ίδια στιγμή, για τους σχεδιαστές αυτών των δικτύων, αποτελεί σοβαρό πρόβλημα το να εντοπίσουν για ποιους ακριβώς λόγους δόθηκε μια τόσο εσφαλμένη απάντηση· ακόμα κι αν «πειράξουν» κάποια βάρη για να «φτιάξουν ένα πρόβλημα», αυτό εύκολα μπορεί να σημαίνει ότι μπορεί να δημιουργήσουν δύο και τρία καινούργια από τη στιγμή που τα ίδια βάρη μπορεί να συμμετέχουν στην κωδικοποίηση πολλαπλών γνώσεων – οι συνάψεις που έχουν «μάθει» τα σχετικά με το βάρος του ατσαλιού ενδέχεται να έχουν «μάθει» και τα σχετικά με την κατεργασία του, με αποτέλεσμα τυχόν πείραγμά τους να σημαίνει ότι το δίκτυο, μετά τη «διόρθωση» σχετικά με το βάρος, θα «ξέρει» επίσης ότι το καλύτερο καμίνι για το ατσάλι είναι μια εκκοκιστική μηχανή. Το ευτύχημα σε αυτήν την περίπτωση είναι ότι τέτοιου είδους λάθη εντοπίζονται εύκολα και άμεσα από τους ανθρώπινους χειριστές, ακόμα κι αν η διόρθωσή τους παρουσιάζει προβλήματα. Το δυστύχημα είναι ότι αυτά τα λάθη αποτελούν μόνο μία κατηγορία λαθών από αυτές στις οποίες υποπίπτουν τα γλωσσικά μοντέλα. Υπάρχει και μια κατηγορία πιο ύπουλων λαθών τα οποία, παρότι ίδιας αιτιολογίας με το προηγούμενο παράδειγμα του ατσαλιού, εντοπίζονται πολύ δυσκολότερα, ειδικά όταν το κείμενο που παράγεται αφορά σε πιο εξειδικευμένα ζητήματα. Για να δώσουμε ένα κάπως γκροτέσκο και μάλλον υπερβολικό παράδειγμα, έστω ότι ένα γλωσσικό μοντέλο παράγει τη φράση «η ακετυλχολίνη είναι ένας νευροδιαβιβαστής που παράγεται στους λεμφαδένες, διαχέεται μέσω του κυκλοφορικού και ρυθμίζει την παραγωγή ωαρίων στις ωοθήκες». Προφανώς, για κάποιον σχετικά αδαή με τα ζητήματα της ανθρώπινης φυσιολογίας, μια τέτοια φράση μοιάζει πολύ «επιστημονική» και αληθοφανής. Στην πραγματικότητα, πρόκειται για ένα έκτρωμα χωρίς απολύτως καμμία βάση που χρειάζεται ένα κάπως πιο εξοικειωμένο μάτι για να εντοπιστεί ως τέτοιο. Τα γλωσσικά μοντέλα ωστόσο δεν έχουν κανέναν ενδοιασμό να παράγουν τέτοιες «γνώσεις» (αν και ίσως όχι τόσο χοντροκομμένες), παραθέτοντας μάλιστα και σχετική βιβλιογραφία, η οποία όμως μπορεί στην ουσία να λέει τα ακριβώς αντίθετα, γεγονός που τα μοντέλα δεν μπορούν να αντιληφθούν.

Το ζήτημα γίνεται ακόμα πιο «γαργαλιστικό» στις περιπτώσεις όπου το κείμενο που παράγεται περιέχει σε μεγάλο βαθμό επακριβείς πληροφορίες (πείθοντας έτσι αρχικά ακόμα κι έναν ειδικό) ενώ ταυτόχρονα μπορεί να έχουν παρεισφρήσει σε αυτό εδώ κι εκεί μερικές «αστοχίες» (και αυτές ωστόσο πάντα τεκμηριωμένες, με παραπομπές σε πηγές). Υπό το καθεστώς μιας διάχυτης καχυποψίας για την ακρίβεια των όσων «λέει ο στόμας» αυτών των μοντέλων δεν μπορεί φυσικά να γίνεται λόγος για ενδεχόμενη χρήση τους (τουλάχιστον προς το παρόν) σε οποιονδήποτε τομέα απαιτεί έναν ελάχιστο βαθμό αξιοπιστίας (π.χ., για ιατρικές διαγνώσεις).

Για τους υπερμάχους των βαθιών νευρωνικών δικτύων, η λύση σε τέτοια προβλήματα είναι προφανής: χρειαζόμαστε περισσότερα δεδομένα για να εκπαιδεύονται τα δίκτυα και ίσως ακόμα και μεγαλύτερα δίκτυα. Δεν πρόκειται για εντελώς αβάσιμη θέση· τα άλματα που έχουν κάνει τα νευρωνικά δίκτυα τα τελευταία χρόνια οφείλονται σε μεγάλο βαθμό στο γεγονός ότι ανακαλύφθηκαν νέες αρχιτεκτονικές και νέες τεχνικές που τους επιτρέπουν να καταναλώνουν τεράστιους όγκους δεδομένων, σαν αυτούς που παράγονται πλέον από κάθε μικρή ή μεγάλη συσκευή. Μέχρι ποιο σημείο μπορεί να φτάσει όμως αυτή η λογική της μεγέθυνσης; Κάποιες πρώτες έρευνες υποδεικνύουν ότι ενδεχομένως τα νευρωνικά δίκτυα να τρέχουν ήδη στα όριά τους σε σχέση με το οριακό όφελος που αποκομίζουν από τακτικές μεγέθυνσης. Από μια πιο φιλοσοφική και πολιτική άποψη, η αντίληψη ότι η μάθηση και η ευφυΐα είναι αποτέλεσμα απλής συσσώρευσης εμπειρικών δεδομένων προϋποθέτει κάποιες ανθρωπολογικού τύπου παραδοχές που δεν είναι καθόλου αυτονόητες. Πρόκειται φυσικά για την παλιά και καλή εκείνη ακραία εκδοχή του εμπειρισμού που γνώρισε (και συνεχίζει να γνωρίζει) μεγάλη επιτυχία στον αγγλοσαξωνικό χώρο: όλος ο κόσμος κατασκευάζεται πάνω σε συμβάσεις που οι άνθρωποι αποδέχονται (καμμία έννοια περί a priori κατηγοριών δεν νοείται ευλογοφανής) και οι οποίες μπορούν να γίνουν αντικείμενο μάθησης απλώς και μόνο μέσω της έκθεσης στα σχετικά δεδομένα. Αυτή η εμπειρικού τύπου συμβασιοκρατία αυτόματα συνεπάγεται ότι και το υποκείμενο της μάθησης δεν έχει «προ-εγκατεστημένες» αντιλήψεις και ότι διαθέτει μια εξαιρετική πλαστικότητα – όχι τυχαία, η έννοια της πλαστικότητας στις νευροεπιστήμες κατέχει εξέχουσα θέση τα τελευταία χρόνια.

Για ορισμένους σαν τον Marcus που αναφέραμε παραπάνω, μια εναλλακτική θα ήταν να συνδυαστούν τα νευρωνικά δίκτυα με συστήματα συμβολικής λογικής, δηλαδή συστήματα που εργάζονται απευθείας πάνω σε λογικού τύπου κανόνες (κάπως πιο περίπλοκους από αυτές της άλγεβρας Boole) και που κάποτε, πριν την πρόσφατη έκρηξη των νευρωνικών, υπήρξαν αρκετά δημοφιλή στον χώρο της τεχνητής νοημοσύνης. Η ελπίδα είναι ότι, αν ο τεχνητός εγκέφαλος είναι εξοπλισμένος με λογικούς κανόνες, τότε θα μπορεί να αποφύγει τα εμφανώς παράλογα συμπεράσματα στα οποία φτάνουν ενίοτε τα νευρωνικά. Ακόμα κι αν όντως προσφέρει κάποια πλεονεκτήματα ο συνδυασμός νευρωνικών δικτύων και συμβολικής λογικής, δεν είναι καθόλου βέβαιο ότι θα αποφευχθούν τα παράλογα συμπεράσματα. Ο λόγος είναι ότι η αποτίμηση ενός συμπεράσματος ως λογικού ή παράλογου δεν γίνεται αποκλειστικά και μόνο στο επίπεδο της τυπικής λογικής – όπως έχουν δείξει ο Mauss και ο Durkheim, ο τρόπος που δομείται μια συγκεκριμένη λογική και οι βασικές της κατηγορίες δεν είναι ποτέ απαλλαγμένος από κοινωνικές επιρροές, από τις ανάγκες της κοινωνικής ομάδας που χρησιμοποιεί τη συγκεκριμένη λογική. Δεν είναι καθόλου σπάνιο (είτε ως ανθρωπολογικό φαινόμενο σε μακρινές και «εξωτικές» κοινωνίες είτε ακόμα και ως φαινόμενο της καθημερινής κοινωνικής επαφής στις δυτικές κοινωνίες) μια συζήτηση να καταλήγει σε ένα συμπέρασμα με τυπικά σωστό τρόπο (π.χ., ότι η ιδέα του Soylent Green είναι εξαιρετική και πρέπει να τεθεί άμεσα σε εφαρμογή), αλλά αυτό το συμπέρασμα να μη γίνεται αποδεκτό από μερικούς εκ των συνομιλητών για λόγους έξω-λογικούς (όχι παράλογους όμως)· οπότε και ξεκινάει μια διαδικασία ανεύρεσης εξαιρέσεων και ιδιαιτεροτήτων ώστε να σπάσει σε μερικά σημεία της η λογική αλυσίδα που οδηγεί στο (κοινωνικά) εμφανώς παράλογο συμπέρασμα.

Ένα διαφορετικό ζήτημα που δεν λύνει η προσθήκη της συμβολικής λογικής αφορά στο κατά πόσον αυτό που καλείται «νοημοσύνη» ανάγεται σε χειρισμούς αριθμών και συμβόλων, ερήμην του σώματος και των δικών του απαιτήσεων και δυνατοτήτων. Θα ήταν μάλλον υπερβολικό να ισχυριστεί κανείς ότι μια ευφυής κίνηση που κάνει ένας αθλητής στο γήπεδο γίνεται κατόπιν λογικών και αριθμητικών υπολογισμών εκ μέρους του (ή ότι οι σωματικές κινήσεις δεν αποτελούν καν δείγμα νοημοσύνης). Από την άλλη, η υπόθεση ότι τέτοιοι υπολογισμοί ενδεχομένως γίνονται σε ασυνείδητο επίπεδο, παρότι ευλογοφανής, θα έπρεπε τουλάχιστον να επιβεβαιωθεί στην πράξη, κάτι που δεν έχει γίνει μέχρι σήμερα. Όπως εννοείται σήμερα, η «νοημοσύνη», παρά το ότι κατανοείται κατά βάση εμπειριστικά, ταυτόχρονα ενσωματώνει τον κλασσικό δυισμό σώματος και πνεύματος, με το δεύτερο φυσικά να έχει τον πρωτεύονται ρόλο [3Υπάρχει και ο (κάπως πιο περιθωριοποιημένος) κλάδος της λεγόμενης ενσώματης νόησης (embodied cognition) που θεωρεί το σώμα εκ των ων ουκ άνευ για την ανάδυση της νοημοσύνης. Συνεπώς, θεωρεί ότι τα ρομπότ, με την υλικότητά τους, είναι ο καταλληλότερος δρόμος προς την κατασκευή σκεπτόμενων μηχανών. Παρότι πιο ενδιαφέρουσα αυτή η προσέγγιση, παραμένει το ζήτημα του πώς ένα υλικό κατασκεύασμα, όπως ένα ρομπότ, θα μπορούσε να αναπτύξει κάποια βασικά «ένστικτα» και ένα αξιακό σύστημα που θα του επιτρέπουν να κινείται στον και να αλληλεπιδρά με τον κόσμο. Το να εισαχθούν κάποιοι προγραμματιστικοί κανόνες στον «εγκέφαλο» ενός ρομπότ, τύπου «να αποφεύγεις κινήσεις που μπορεί να σε βλάψουν», ως μετωνυμία της ανάγκης αυτοσυντήρησης, θα ήταν μια κάποια λύση σε τεχνικό επίπεδο, η οποία ωστόσο δεν φαντάζει και πολύ πειστική από φιλοσοφική άποψη.].

Ένας βασικός λόγος για τον οποίο σύγχρονα συστήματα τεχνητής νοημοσύνης, όπως τα μεγάλα γλωσσικά μοντέλα, προκαλούν τέτοια αναστάτωση έχει να κάνει με αυτόν τον βαθιά αφομοιωμένο δυϊσμό σώματος – πνεύματος που ακόμα διακρίνει τις δυτικές κοινωνίες, παρά τους όρκους πίστης που κατά καιρούς αφιερώνουν σε διάφορες υλιστικές φιλοσοφίες. Η αυτοματοποίηση και η ρομποτοποίηση της γραμμής παραγωγής κατά την 3η βιομηχανική επανάσταση παρήγαγε κάποιες ανασφάλειες για τις (χειρωνακτικές) δουλειές που θα χάνονταν, αλλά όχι μια αίσθηση υπαρξιακής απειλής (αυτή έβρισκε σε έναν βαθμό δίοδο έκφρασης κυρίως στην τέχνη). Τα μεγάλα γλωσσικά μοντέλα δεν χειρίζονται απλώς ρομποτικούς βραχίονες, δεν αναγνωρίζουν σηματάκια σε εικόνες ούτε μερικές φωνητικές εντολές. Αντιθέτως, δίνουν την εντύπωση ότι παράγουν λόγο με νόημα και ότι μπορούν να κάνουν στο «πνεύμα» ό,τι έκανε ο ταιηλορισμός στο σώμα. Με αυτόν τον τρόπο πλήττουν ένα από τα τελευταία καταφύγια που είχε διαφυλάξει για τον εαυτό του ο σύγχρονος μέτα-αστός: ότι το πνεύμα του (και η πνευματική εργασία εν γένει) έχει μια ιδιαίτερη θέση έναντι του αναλώσιμου σώματος και ότι πρέπει να τυγχάνει ειδικής μεταχείρισης, ότι με αυτό μπορεί να χτίζει παλάτια και να αυτο-προσδιορίζεται καταπώς το επιθυμεί.

Το πώς ακριβώς θα διαχειριστεί ψυχολογικά ο μετα-αστός τη μετάβαση προς έναν κόσμο όπου τα πτυχία του, η καλλιέργειά του και οι γνώσεις του, όπως τα ήξερε μέχρι τώρα, θα έχουν πλέον μικρό αντίκρυσμα είναι ένα ζήτημα που ίσως να μην αφορά ιδιαίτερα και πολλούς πέρα από τον ίδιο. Το βέβαιο είναι ότι θα βρεθεί κάποια άλλη κατάλληλη και βολική ιδεολογία να εξυπηρετήσει τέτοιες ανάγκες. Ωστόσο, το ζήτημα της μηχανοποίησης της γλώσσας αυτό καθεαυτό είναι πολύ ευρύτερο από τις ανησυχίες του όποιου κατά φαντασίαν «πνευματικού» ανθρώπου. Ένα παράδειγμα εφαρμογής των νέων τεχνικών μηχανοποίησης της γλώσσας αφορά και στην παραγωγή λογοτεχνικών προϊόντων. Εργαλεία όπως τα ChatGPT και GPT-3 χρησιμοποιούνται τα τελευταία χρόνια για να παρέχουν μια χείρα βοηθείας σε επίδοξους συγγραφείς όταν αυτοί μπλοκάρουν και δεν μπορούν να βρούνε μια καινούρια ιδέα, όταν βαριούνται να ασχοληθούνε με κάποια πιο τετριμμένα κομμάτια του βιβλίου τους (π.χ., με την περιγραφή μιας πόλης) και γενικά οποτεδήποτε έχουν ανάγκη από μια αύξηση της παραγωγικότητάς τους· συνήθως πρόκειται για συγγραφείς που εξειδικεύονται σε συγκεκριμένα είδη (π.χ., high fantasy, cyber noir), έχουν συγκεκριμένο κοινό με τις δικές του απαιτήσεις και που πρέπει να παράγουν νέους τόμους σχεδόν με ρυθμούς τηλεοπτικής σειράς – κάποιοι από αυτούς έχουν υπολογίσει ότι αν καθυστερήσουν να βγάλουν το επόμενο βιβλίο τους περισσότερο από τέσσερις μήνες, αυτό θα σημάνει και μια μείωση του κοινού τους και άρα και των εσόδων τους. Όμως τα κείμενα που «γράφουν» αυτοί οι συγγραφείς έχουν παραχθεί από εργαλεία που με τη σειρά τους έχουν εκπαιδευτεί πάνω σε κειμενικά δεδομένα, δηλαδή σε παλαιότερα λογοτεχνικά κείμενα, γραμμένα από ανθρώπινο χέρι. Σε ποιον επομένως ανήκουν τα δικαιώματα του παραχθέντος κειμένου; Στους αρχικούς συγγραφείς που δώσανε κείμενα για την εκπαίδευση των μοντέλων, στους συγγραφείς που χρησιμοποίησαν αυτά τα μοντέλα ή μήπως και στους μηχανικούς που τα σχεδίασαν; Αργά ή γρήγορα θα επιλυθούν και τα όποια νομικά προβλήματα ανακύψουν [4Η πρώτη σχετική νομική διαμάχη έχει ήδη ξεκινήσει στη Βρετανία. Αφορά στη χρήση εικόνων από τη σελίδα Getty (ένα από τα μεγαλύτερα αποθετήρια πρωτότυπων εικόνων) για την εκπαίδευση μοντέλων παραγωγής εικόνων και στο ζήτημα του σε ποιον ανήκουν τα δικαιώματα των νέων εικόνων ή αν οι εταιρείες που χρησιμοποιούν τις πρωτότυπες εικόνες ως «εκπαιδευτικό κιμά» έχουν το δικαίωμα να το πράξουν αυτό άνευ άδειας. Βλ. το άρθρο στους Financial Times “Art and artificial intelligence collide in landmark legal dispute”.].

Από πολιτική άποψη ωστόσο, είναι μάλλον κρισιμότερο το ότι αυτά τα γλωσσικά μοντέλα λειτουργούν ως μηχανές πρωταρχικής συσσώρευσης· συσσώρευσης του γλωσσικού πλούτου. Σε κάποιους θα μπει βέβαια η ιδέα ότι, για να είναι δίκαιη αυτή η διαδικασία, θα πρέπει ίσως να αποζημιώνονται όσοι θα παράγουν πρωτογενή γλωσσικά δεδομένα (δηλαδή δυνητικά όσοι μιλάνε). Παρόμοιες ιδέες έχουν άλλωστε ήδη διατυπωθεί γενικά για τα δεδομένα κίνησης. Όσο βέβαια προστατεύτηκαν οι αγρότες από τις περιφράξεις στην Αγγλία επειδή θεσπίστηκε κάποιο αγροτικό δίκαιο, άλλο τόσο αναμένεται να προστατευτούν και όσοι μιλάνε την τάδε ή δείνα γλώσσα. Η φωνή της μηχανής προβλέπεται εξάλλου να είναι πολύ γλυκιά και «ασφαλής», χωρίς ιδεολογικά παραστρατήματα και διανοητικούς πειρασμούς, πάντα στο όνομα της διαφορετικότητας και της συμπερίληψης.

Separatrix

Σημειώσεις

1 - Όλες οι εικόνες που συνοδεύουν το κείμενο, εκτός από τα διαγράμματα των νευρωνικών δικτύων, έχουν παραχθεί από μας με τη βοήθεια του DALL-E 2, ενός μοντέλου τεχνητής νοημοσύνης που παράγει εικόνες με βάση μια περιγραφή που δίνει ο χρήστης υπό τη μορφή κειμένου.
[ επιστροφή]

2 - Βλ. σχετικά και το άρθρο «Σκάνδαλο LaMDA βλέπουν εφιάλτες τα νευρωνικά τεχνοδίκτυα;)», cyborg 25.
[ επιστροφή]

3 - Υπάρχει και ο (κάπως πιο περιθωριοποιημένος) κλάδος της λεγόμενης ενσώματης νόησης (embodied cognition) που θεωρεί το σώμα εκ των ων ουκ άνευ για την ανάδυση της νοημοσύνης. Συνεπώς, θεωρεί ότι τα ρομπότ, με την υλικότητά τους, είναι ο καταλληλότερος δρόμος προς την κατασκευή σκεπτόμενων μηχανών. Παρότι πιο ενδιαφέρουσα αυτή η προσέγγιση, παραμένει το ζήτημα του πώς ένα υλικό κατασκεύασμα, όπως ένα ρομπότ, θα μπορούσε να αναπτύξει κάποια βασικά «ένστικτα» και ένα αξιακό σύστημα που θα του επιτρέπουν να κινείται στον και να αλληλεπιδρά με τον κόσμο. Το να εισαχθούν κάποιοι προγραμματιστικοί κανόνες στον «εγκέφαλο» ενός ρομπότ, τύπου «να αποφεύγεις κινήσεις που μπορεί να σε βλάψουν», ως μετωνυμία της ανάγκης αυτοσυντήρησης, θα ήταν μια κάποια λύση σε τεχνικό επίπεδο, η οποία ωστόσο δεν φαντάζει και πολύ πειστική από φιλοσοφική άποψη.
[ επιστροφή]

4 - Η πρώτη σχετική νομική διαμάχη έχει ήδη ξεκινήσει στη Βρετανία. Αφορά στη χρήση εικόνων από τη σελίδα Getty (ένα από τα μεγαλύτερα αποθετήρια πρωτότυπων εικόνων) για την εκπαίδευση μοντέλων παραγωγής εικόνων και στο ζήτημα του σε ποιον ανήκουν τα δικαιώματα των νέων εικόνων ή αν οι εταιρείες που χρησιμοποιούν τις πρωτότυπες εικόνες ως «εκπαιδευτικό κιμά» έχουν το δικαίωμα να το πράξουν αυτό άνευ άδειας. Βλ. το άρθρο στους Financial Times “Art and artificial intelligence collide in landmark legal dispute”.
[ επιστροφή]